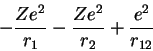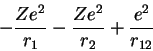Next: The Expansion of a
Up: Legendre Polynomials, Generating Functions
Previous: A Generating Function for
Another method of introducing Legendre Polynomials is through the dipole moment generating
function.
Since this method is very important in Quantum Mechanical computations concerning
poly-electronic atoms and molecules, it is worth our attention.
When one considers the Hamiltonian of the Helium Atom's electrons (for example), one has
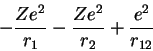 |
(4) |
where r12 is the distance between electron 1 and electron 2, i.e., it is
the electron-electron repulsion term.
We examine this term in this discussion.
We can write this electron-electron repulsion term as
 |
(5) |
where r1 and r2 are the distances from the nucleus to electrons 1 and 2 respectively.
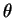 is the angle between the vectors from the nucleus to electron 1 and electron 2.
It is required that we do this is two domains, one in which r1>r2 and one in which r2>r1.
This is done for convergence reasons (vide infra).
For the former case, we define
is the angle between the vectors from the nucleus to electron 1 and electron 2.
It is required that we do this is two domains, one in which r1>r2 and one in which r2>r1.
This is done for convergence reasons (vide infra).
For the former case, we define
so that 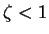 < 1$">,
and Equation 5
becomes
< 1$">,
and Equation 5
becomes
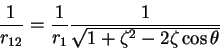 |
(6) |
which we now expand in a power series in
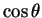 (which will converge while
(which will converge while 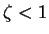 < 1$">).
We have
< 1$">).
We have
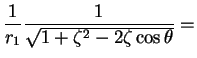 |
|
|
(7) |
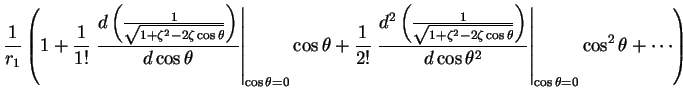 |
|
|
(8) |
It is customary to change notation from
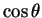 to
to 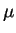 ,
so
,
so
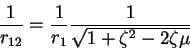 |
(9) |
which we now expand in a power series in 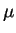 (which will converge while
(which will converge while 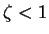 < 1$">).
We have
< 1$">).
We have
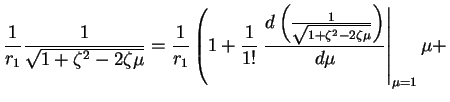 |
|
|
|
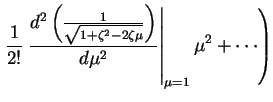 |
|
|
(10) |
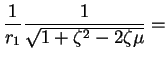 |
|
|
|
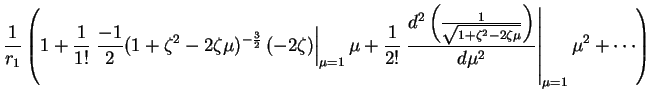 |
|
|
(11) |
which is
i.e.,
which is, after the second differentiation
Dropping the r1 term, we have



Next: The Expansion of a
Up: Legendre Polynomials, Generating Functions
Previous: A Generating Function for
2001-12-13