


Next: About this document ...
Up: An Alternative Generating Function
Previous: An Alternative Generating Function
There is yet another way to see Legendre Polynomials in action, through the
expansion of the potential energy of point dipoles.
To start, we assume that we have a dipole at the origin, with its
positive charge (q) at (0,0,-a/2) and its negative charge (-q) at (0,0,+a/2), so
that the ``bond length'' is ``a'', and therefore the ``dipole moment''
is ``q a''.
At some point P(x,y,z), located (also) at r,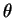 ,
,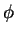 ,
we have
that the potential energy due to these two point charges is
,
we have
that the potential energy due to these two point charges is
which is just Coulomb's law.
If we expand this potential energy as a function of ``a'', the ``bond distance'', we have
All we need do, now, is evaluate these derivatives.
We have, for the first
which is,
in the limit
 ,
,
so, we have, so far,
i.e., to the dipolar form.
For the second derivative, we take the derivative of the
first derivative:
which equals zero.
The next term gives
and so it goes.



Next: About this document ...
Up: An Alternative Generating Function
Previous: An Alternative Generating Function
2001-12-13
![]() ,
,![]() ,
we have
that the potential energy due to these two point charges is
,
we have
that the potential energy due to these two point charges is
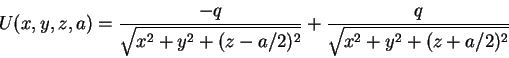
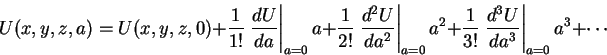
![\begin{displaymath}\frac{1}{1!}\left . \frac{d U}{da}\right \vert _{a=0} =
q \le...
...{1}{2})}{(x^2+y^2+(z+a/2)^2))^{\frac{3}{2}}} \right ]
\right )
\end{displaymath}](img36.gif)
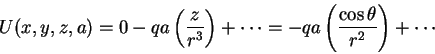
![\begin{displaymath}\frac{1}{2!}\left . \frac{d \frac{dU}{da}}{da}\right \vert _{...
...^2+(z+a/2)^2))^{\frac{3}{2}}} \right ] \right )}
{da}
\right )
\end{displaymath}](img40.gif)