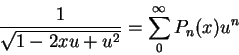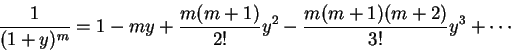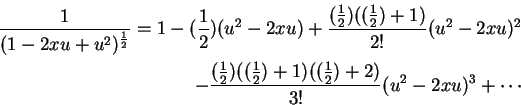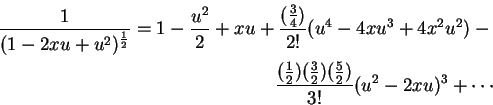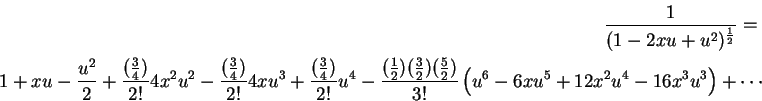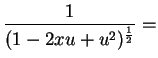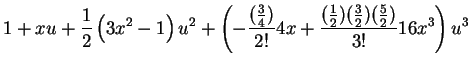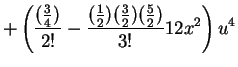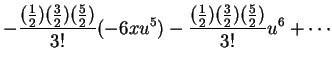Next: An Alternative Generating Function
Up: Legendre Polynomials, Generating Functions
Previous: Legendre Polynomials, Generating Functions
The technically correct generating function for Legendre polynomials is
obtained using the equation
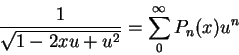 |
(1) |
We expand the denominator using the binomial theorem,
where
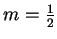 and the series converges when y<1.
Notice that it is an alternating series.
Identifying
y = u2-2xu we have
and the series converges when y<1.
Notice that it is an alternating series.
Identifying
y = u2-2xu we have
which we now re-arrange in powers of u
(in the mode required by Equation 1), obtaining
which is, rearranging
or, collecting terms in powers of u, we have
where the quadratic terms (in u, i.e. 3x2-1) is the familiar spherical harmonic associated with
the dz2 orbital, among other things.



Next: An Alternative Generating Function
Up: Legendre Polynomials, Generating Functions
Previous: Legendre Polynomials, Generating Functions
2001-12-13