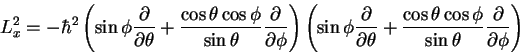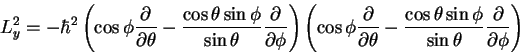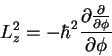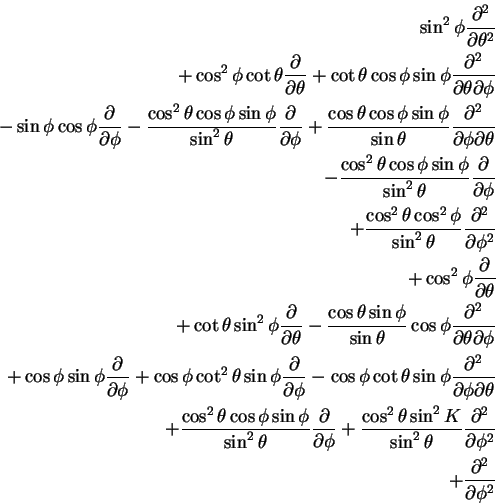Next: .
Up: Alternative Formulations for Angular Operators
Previous: .
We need to form L2, i.e.,
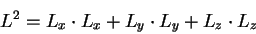 |
(23) |
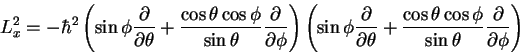 |
(24) |
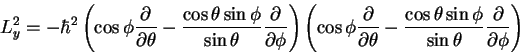 |
(25) |
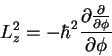 |
(26) |
For Lx2 we have, upon expansion
For Ly we have
and, of course
It follows, adding
Equations 27, 28 and 7, that



Next: .
Up: Alternative Formulations for Angular Operators
Previous: .
2001-12-26