


Next: .
Up: Revisiting Woodward Hoffmann Rules
Previous: .
or
Figure 9:
Overlap Integral as a function of Internuclear Distance.
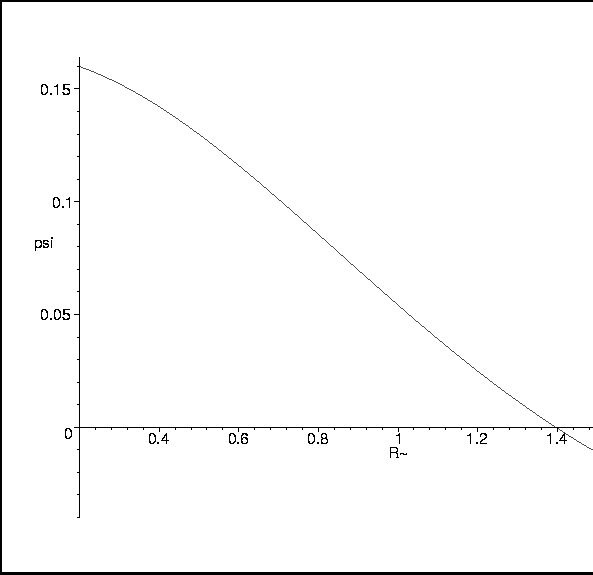 |
Figure 10:
Overlap Integral as a function of Internuclear Distance and
Exponent in Wave Function.
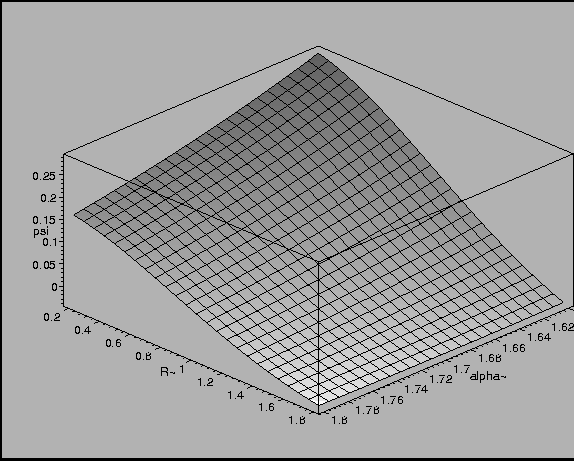 |
This term is sometimes positive and sometimes negative depending on 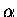 and R.
So, the argument, that
and R.
So, the argument, that 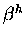 is somehow proportional to the overlap, fails.
is somehow proportional to the overlap, fails.
Assume the ``horizontal''
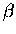
is negative
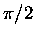 the four
ground state electrons remain in the ground state, switching
identity, but no more
(see Figure 11).
the four
ground state electrons remain in the ground state, switching
identity, but no more
(see Figure 11).
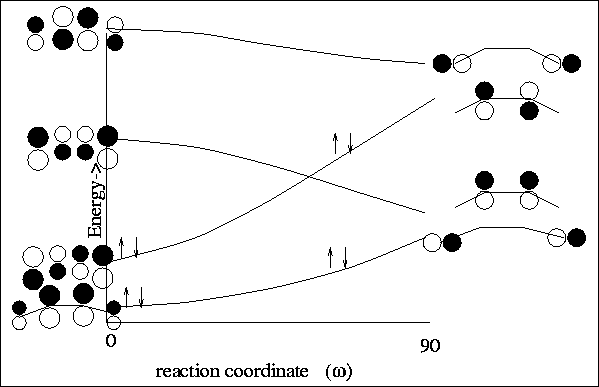
For the con-rotatory ring closure, one sees that the ground state electrons
find themselves in an excited state of the cyclic product
(see Figure 12).
Assume the ``horizontal''
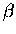
is positive
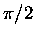 .
The ground state electrons find themselves promoted to an excited state
(see Figure 12).
.
The ground state electrons find themselves promoted to an excited state
(see Figure 12).
For the con-rotatory ring closure, we find that the
ground state electrons
adiabatically remaining in a ground state configuration
(see Figure 11).
Clearly, given these diagrams, it is very important what the sign
of 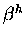 is!
is!
Figure:
Disrotatory ring closure, 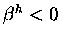 <0$">
and
Conrotatory ring closure,
<0$">
and
Conrotatory ring closure, 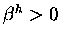 0$">.
The latter corresponds to the thermally allowed ring
closure predicted by Woodward and Hoffmann.
0$">.
The latter corresponds to the thermally allowed ring
closure predicted by Woodward and Hoffmann.
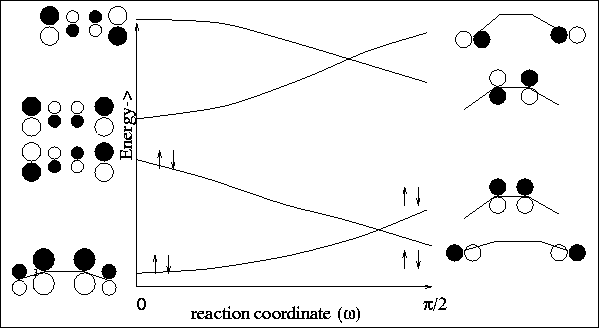 |
Figure:
Conrotatory ring closure, 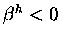 <0$">
Disrotatory ring closure,
<0$">
Disrotatory ring closure, 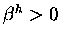 0$">
0$">
 |



Next: .
Up: Revisiting Woodward Hoffmann Rules
Previous: .
Carl David
1999-06-16
![]() and R.
So, the argument, that
and R.
So, the argument, that ![]() is somehow proportional to the overlap, fails.
is somehow proportional to the overlap, fails.
![]() is!
is!
