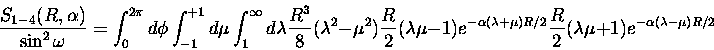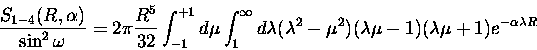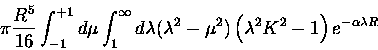Next: .
Up: Revisiting Woodward Hoffmann Rules
Previous: .
We now have, substituting appropriately into Equation
19,
where we have dropped the partial derivative with respect to 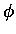 term
since we are dealing with
term
since we are dealing with 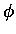 independent
independent 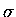 states (
states (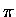 states
and higher need to include this term!)
resulting in a function for
states
and higher need to include this term!)
resulting in a function for
 .
We would then have to assume an R value (based on the C-C bond length),
and an
.
We would then have to assume an R value (based on the C-C bond length),
and an 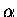 value, presumably obtained through variational calculations.
Standard practice instead is to assign a value
from thermochemical considerations.
value, presumably obtained through variational calculations.
Standard practice instead is to assign a value
from thermochemical considerations.
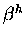 is sometimes thought of as being
proportional to the overlap, so that twisting the
bond involved results in decrease in both the resonance
integral and the overlap.
is sometimes thought of as being
proportional to the overlap, so that twisting the
bond involved results in decrease in both the resonance
integral and the overlap.
At the termini of the molecule, we would have
Let us calculate the overlap between
ph1 and ph4 and ask if the
appropriate Hamiltonian matrix element can be proportional
to this overlap.
We have (in analogy with the development of H1-4 (above)
that the integral we need to evaluate is
for controtatory ring closure.
where we have explicitly shown which variables will remain after integration.
We rewrite this equation as
which becomes



Next: .
Up: Revisiting Woodward Hoffmann Rules
Previous: .
Carl David
1999-06-16
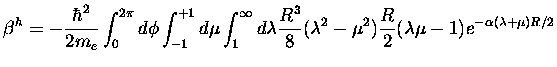
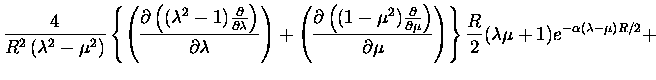
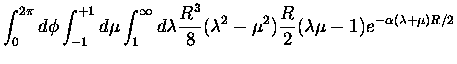
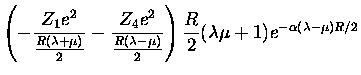
![]() is sometimes thought of as being
proportional to the overlap, so that twisting the
bond involved results in decrease in both the resonance
integral and the overlap.
is sometimes thought of as being
proportional to the overlap, so that twisting the
bond involved results in decrease in both the resonance
integral and the overlap.