.

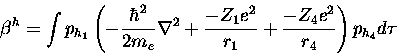$$\beta^h = \int p_{h_1} \left ( -\frac{\hbar^2}{2 m_e} \nabla... ...Z_1 e^2 }{r_1} +\frac{-Z_4 e^2 }{r_4} \right ) p_{h_4} d\tau$$ (19)

(note that Z₁=Z₄ in our case) with the appropriate kinetic energy operator, potential energy operator, differential volume element, and total wave function, in elliptical coordinates. The two appropriate wave functions are

$$p_{h_1} = (z-R/2)e^{-\alpha r_1} = \frac{R}{2}(\lambda \mu - 1) e^{-\alpha (\lambda + \mu)R/2}$$

and

$$p_{h_4} = (K+R/2)e^{-\alpha r_4} = \frac{R}{2}(\lambda \mu + 1) e^{-\alpha (\lambda - \mu)R/2}$$