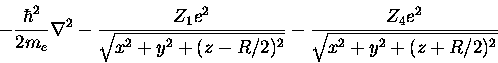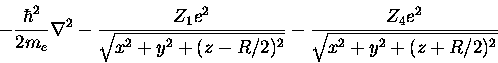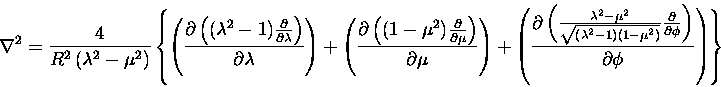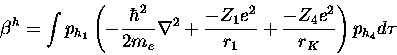Next: .
Up: Revisiting Woodward Hoffmann Rules
Previous: What is the sign
Brute force integration usually requires that we first transform to
elliptical
coordinates, where
and
(and 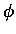 ,
the common azimuthal angle taken from spherical polar coordinates is a hold over)
or, conversely,
,
the common azimuthal angle taken from spherical polar coordinates is a hold over)
or, conversely,
and
This is covered elsewhere in the Computer Guided Reading set of readings.
In order to proceed with the evaluation of the integral,
we convert to this new coordinate system, where
and
we then form (from Equation 18)
Carl David
1999-06-16