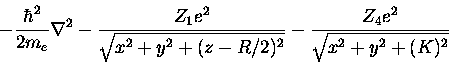Next: .
Up: Revisiting Woodward Hoffmann Rules
Previous: .
We need to establish a value for 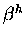 .
Technically,
.
Technically, 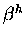 corresponds to evaluating an integral
(see C. W. David, J. Chem. Ed., 59, 288 (1982) and
C. W. David, J. Chem. Ed., 68, 129 (1991))
such as
corresponds to evaluating an integral
(see C. W. David, J. Chem. Ed., 59, 288 (1982) and
C. W. David, J. Chem. Ed., 68, 129 (1991))
such as
 |
(18) |
where r1 and r4 are the distances from
nucleus 1 and 4 respectively to the electron,
and R is the distance between the carbon atoms one and four.
In a consistent coordinate system (x,y,z),
using the coordinate system previously defined
(the relevant carbon atoms are located at (0,0,R/2) and (0,0,-R/2)).
This is the reason why we chose to place Carbons 1 and 4 on the z-axis.
Otherwise, we would have to have written things like
where 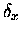 and
and 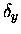 were offset coordinates for the x- and y-
directions, similar to the R/2 offset term for the z- coordinates.
The one-electron Hamiltonian Operator (in the same coordinate system) is
were offset coordinates for the x- and y-
directions, similar to the R/2 offset term for the z- coordinates.
The one-electron Hamiltonian Operator (in the same coordinate system) is



Next: .
Up: Revisiting Woodward Hoffmann Rules
Previous: .
Carl David
1999-06-16
![]() .
Technically,
.
Technically, ![]() corresponds to evaluating an integral
(see C. W. David, J. Chem. Ed., 59, 288 (1982) and
C. W. David, J. Chem. Ed., 68, 129 (1991))
such as
corresponds to evaluating an integral
(see C. W. David, J. Chem. Ed., 59, 288 (1982) and
C. W. David, J. Chem. Ed., 68, 129 (1991))
such as