


Next: .
Up: Revisiting Woodward Hoffmann Rules
Previous: Revisiting Woodward Hoffmann Rules
This is an enlarged version of the J. Chem. Ed. article of the same
name, J. Chem. Ed., xx,yy(1999).
The
Hückel theory is applied to electrocyclization
reactions of the Woodward-Hoffmann type.
Introduction
The Woodward-Hoffmann
(R. B. Woodward and R. Hoffmann, "The Conservation of Orbital Symmetry",
Verlag Chemie, Weinhein/Bergstr, 1970)
rules for electrocyclization
reactions
provide an example of Hückel type computations
(see also, J. J. Vollmer and K. L. Servis, J. Chem. Ed., 45, 214 (1968)).
Recent interest
(J. M. Oliva, J. Gerratt, P. B. Karadakov, and D. L. Cooper, J. Chem. Phys.,
107, 8917 (1997),
R. Tian et al. J. A. C. S., 120, 6187 (1998))
in these kinds of reactions makes this discussion even more
germane.
Following Woodward and Hoffmann's example
we employ the electrocylic
reaction of forming a single bond between termini of a system containing
four carbon atoms, each sp2 hydridized, with their 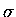 bond skeleton
essentially ``frozen'', and each contributing a p-electron, i.e.,
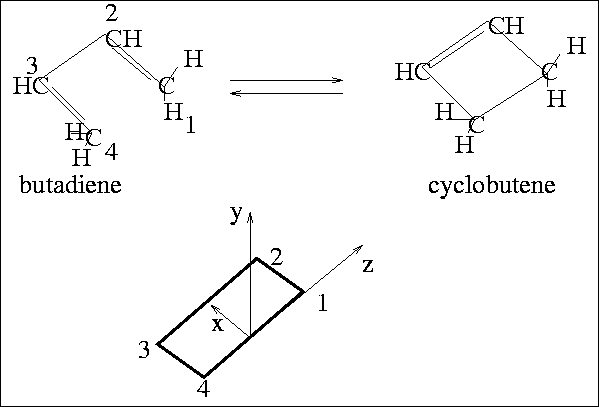
the example concerns the
conversion of butadiene to cyclobutene
(see Figure 1).
We remove the protons
(these protons are often used as markers to distinguish con- and dis-rotatory
motions in qualitative discussions.)
for clarity and
focus entirely on the
bond skeleton
essentially ``frozen'', and each contributing a p-electron, i.e.,
the example concerns the
conversion of butadiene to cyclobutene
(see Figure 1).
We remove the protons
(these protons are often used as markers to distinguish con- and dis-rotatory
motions in qualitative discussions.)
for clarity and
focus entirely on the 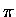 and p orbital structure.
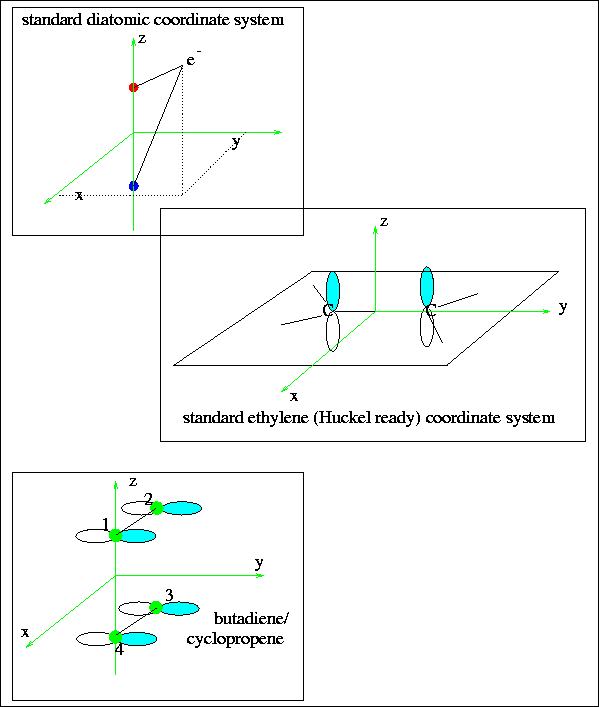
We define the molecule's
plane as containing the x and z axes, with the y-axis perpendicular to that plane;
carbons 1 and 4 define the z-axis, and the x-y plane bisects the 1-4 line.
This means that we are dealing with
py orbitals
when we do normal Hückel computations.
and p orbital structure.
We define the molecule's
plane as containing the x and z axes, with the y-axis perpendicular to that plane;
carbons 1 and 4 define the z-axis, and the x-y plane bisects the 1-4 line.
This means that we are dealing with
py orbitals
when we do normal Hückel computations.
Figure 1:
The coordinate system employed.
 |
In diatomic molecules, the z-axis is usually the bond axis, but when we
move to ethylene treatments, the z-axis is reserved for the p-orbitals
which are going to be used to form the 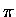 bonds.
It is important to understand that normal Hückel schemes employ pz
orbitals, since these have a simpler form than either px or py.
That means that the ethylene molecule exists in the x-y plane.
bonds.
It is important to understand that normal Hückel schemes employ pz
orbitals, since these have a simpler form than either px or py.
That means that the ethylene molecule exists in the x-y plane.
Figure 2:
The coordinate systems employed for diatomic and Hückel systems.
 |
Here, we change procedures again.
The orbitals in the basis set are going to be py orbitals, rather than
the standard pz orbitals employed in most texts.
Figure:
Naked 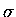 framework and p-electron basis set
framework and p-electron basis set
 |
In Figure 3 we have the two molecules we are considering, and
for comparison sake, we show stretched out butadiene, which is used in
elementary discussions of Hückel MO theory.
The basis set shown, for the linearized butadiene molecule, in normal texts
are pz, but here are py.
In the Hückel computation, the results are a set of energy levels and
coefficients of wave functions.
In Figure 4 are schematically shown the resultant butadiene
MO's (placed according to their relative energies).
Notice that the signs of the coefficients are reflected in the lobe
arrangements (blackened in means +, open means -, or vice versa.
Notice also that the magnitudes of the coefficients reflect in the relative
size of the contributing AO's to the resultant MO's.
Figure 4:
These are the MO's of butadiene, in increasing energy order,
emphasizing both the signs (filled in or empty mirroring + or -).
Included also is the Hamiltonian matrix in the standard Hückel
form.
 |
Defining the Con- and Dis- Processes
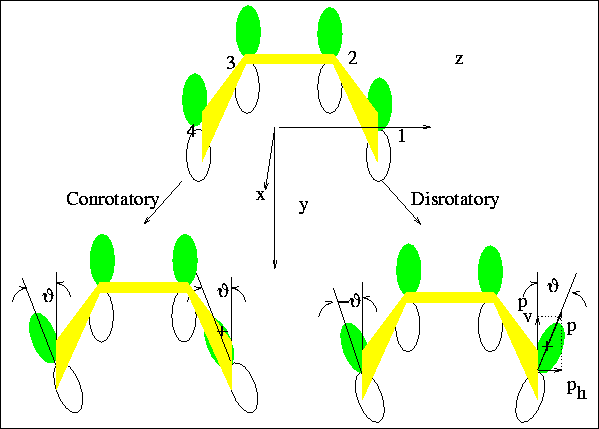
To proceed, we define the twist angles ( 's)
(see Figure 5)
's)
(see Figure 5)
Figure 5:
Defining a Twist Angle
 |
required to follow the reaction in order
to define a reaction coordinate (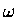 ).
The difference between dis- and con- rotatory motions
is seen in the relationship betweeen the concerted changes in these
).
The difference between dis- and con- rotatory motions
is seen in the relationship betweeen the concerted changes in these  's,
i.e.,
's,
i.e.,
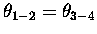 for conrotatory, and
for conrotatory, and
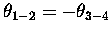 for disrotatory.
Finally, we define an enlarged basis set using pz for
horizontal, and py for vertical normalized p-orbitals.
A generalized orbital (for atoms 1 and/or 4) is
for disrotatory.
Finally, we define an enlarged basis set using pz for
horizontal, and py for vertical normalized p-orbitals.
A generalized orbital (for atoms 1 and/or 4) is



Next: .
Up: Revisiting Woodward Hoffmann Rules
Previous: Revisiting Woodward Hoffmann Rules
Carl David
1999-06-16
![]() bond skeleton
essentially ``frozen'', and each contributing a p-electron, i.e.,
the example concerns the
conversion of butadiene to cyclobutene
(see Figure 1).
We remove the protons
(these protons are often used as markers to distinguish con- and dis-rotatory
motions in qualitative discussions.)
for clarity and
focus entirely on the
bond skeleton
essentially ``frozen'', and each contributing a p-electron, i.e.,
the example concerns the
conversion of butadiene to cyclobutene
(see Figure 1).
We remove the protons
(these protons are often used as markers to distinguish con- and dis-rotatory
motions in qualitative discussions.)
for clarity and
focus entirely on the ![]() and p orbital structure.
We define the molecule's
plane as containing the x and z axes, with the y-axis perpendicular to that plane;
carbons 1 and 4 define the z-axis, and the x-y plane bisects the 1-4 line.
This means that we are dealing with
py orbitals
when we do normal Hückel computations.
and p orbital structure.
We define the molecule's
plane as containing the x and z axes, with the y-axis perpendicular to that plane;
carbons 1 and 4 define the z-axis, and the x-y plane bisects the 1-4 line.
This means that we are dealing with
py orbitals
when we do normal Hückel computations.
