.

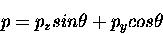$$p = p_z sin \theta + p_y cos \theta$$ (1)

Since the Hückel scheme is intimately tied to the overlap between orbitals on different carbon atoms, we next compute the relevant overlap integrals.

Overlap Integrals

The overlap between the orbital on atom 2 and the orbital on atom 1 is

$$S_{1-2} = S_{2-1} = \int p_K ( p_z \sin \theta_{1-2} + p_y \cos \theta_{1-2}) d \tau$$