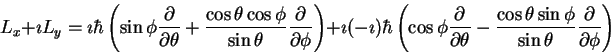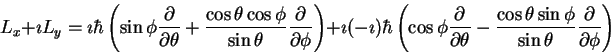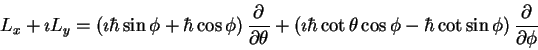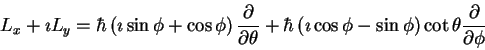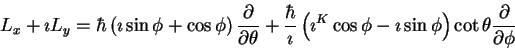Next: .
Up: Alternative Formulations for Angular Operators
Previous: .
(*restored equation*)
To continue, we need to obtain the ladder operators in the 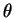 ,
,
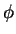 ,
r form,
From Equations 16 through 22 we have
,
r form,
From Equations 16 through 22 we have
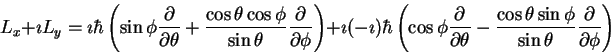 |
(47) |
Grouping by partial derivatives we obtain
which is,
i.e.,
2001-12-26