

Next: Adding, the Cosine
Up: DeMoivre's Theorem
Previous: Derivation
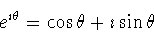 |
(1) |
becomes, upon substituting 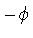 for
for 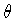
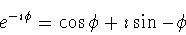 |
(2) |
or,
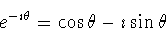 |
(3) |
since it doesn't matter what letter we have on each side of the
equation, and the sine is an odd function (cosine is even).
1998-06-15