

Next: Usage
Up: DeMoivre's Theorem
Previous: Introduction
We start with complex numbers, of the form
which has an Argand diagram which looks like
Figure 1:
Argand Diagram
![\fbox{\includegraphics*[]{argand.ps}}](img2.gif) |
We know that
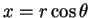 and
and
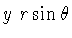 by
elementary trigonomentry, and that the inverse relations obtain
by
elementary trigonomentry, and that the inverse relations obtain
If we expand
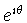 in a Taylor Series
one has
in a Taylor Series
one has
which results in
where we form two alternating series, one imaginary, the other real.
The 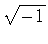 can be factored from the imaginary series, so that we finally obtain
(recognizing the Taylor expansions of sine and cosine)
can be factored from the imaginary series, so that we finally obtain
(recognizing the Taylor expansions of sine and cosine)
which is DeMoivre's (Euler's) Theorem.
1998-06-15
![]() in a Taylor Series
one has
in a Taylor Series
one has