Differential Equations

1.

Given a variable separable differential equation of the form

$$p(V) \frac{dV}{dT} = g(T)$$

where p(V) and g(T) are functions of their respective arguments ONLY, then

$$\int p(V)dV = \int g(T)dT$$

2.

First Order Linear Differential Equations

Given the form

$$\frac{dp(T)}{dT} + g(T)p(T) = q(t)$$

where g(T) and q(T) are KNOWN, GIVEN, functions of T, and one desires to determine p(T), we use integrating factors (h(T)), viz.,

$$h(T) \frac{dp(T)}{dT} + h(T)g(T)p(T) = h(T)q(t)$$

or

$$\frac{dh(T)p(T)}{dT}- \underbrace{p(T) \frac{dh(T)}{dT}} +\underbrace{ h(T)g(T)p(T)} = h(T)q(t)$$

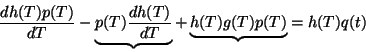
and if the indicated terms could be forced to cancel, i.e.,

$$p(T) \frac{dh(T)}{dT}= h(T)g(T) p(T)$$

then

$$\frac{dh(T)p(T)}{dT} = h(T)q(t) \rightarrow \frac{d\ell n h(T) }{dT} = q(t)$$

which would be integrable