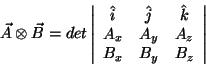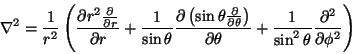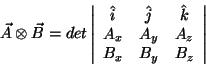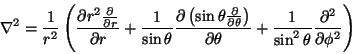Next: About this document ...
Up: Math Review
Previous: Differential Equations
- 1.
- In 2 dimensions,
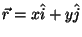 where
where 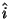 and
and
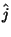 are unit vectors in the i (or x) and j (or y) directions.
are unit vectors in the i (or x) and j (or y) directions.
- 2.
- In 3 dimensions,
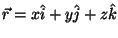 where
where 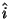 ,
,
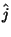 and
and
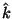 are unit vectors in the i (or x),j (or y), and k (or z) directions.
are unit vectors in the i (or x),j (or y), and k (or z) directions.
- 3.
- The dot product of two vectors
if
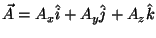 ,
all in 3 dimensions.
,
all in 3 dimensions.
- 4.
- The cross product of two three dimensional vectors
where |A| is the magnitude of 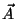 ,
and
,
and
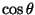 is the angle
between the two vectors. The resultant is itself a vector perpendicular to
both
is the angle
between the two vectors. The resultant is itself a vector perpendicular to
both 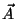 and
and 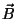 .
.
- 5.
- An alternative representation of the cross product is
- 6.
- In 2 dimensions
- 7.
- In 3 dimensions
- 8.
- In 3 dimensions
which can be re-written in spherical polar coordinates as
2002-06-14