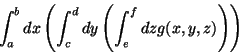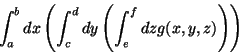Next: Differential Equations
Up: Calculus/Integration
Previous: Calculus/Integration
- 1.
- One dimensional integrals of functions of two (or more) dimensions
are known as ``line integrals''.
One has, given f(x,y),
where ds is the differential element of distance along the specified path
- 2.
- Two dimensional integrals of functions of two dimensions are related
to areas.
If f(x,y) were 1, then this would give the rectangular area bounded by
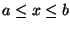 and
and
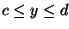 .
.
- 3.
- Three dimensional integrals of functions of 3 dimensions are related
to volumes.
If g(x,y,z) were 1, then this would give the rectangular volume bounded by
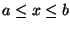 and
and
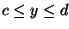 and
and
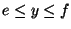 .
.
- 4.
- In two dimensions, one often can use polar coordinates instead of
cartesian, i.e.,
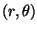 rather than (x,y). The differential area
element changes from dxdy to
rather than (x,y). The differential area
element changes from dxdy to
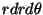 .
.
and
, with
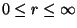 and
and
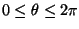 .
.
- 5.
- In 3 dimensions, one often can use spherical polar coordinates
instead of cartesian, i.e.,
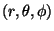 rather than (x,y,z). The
differential volume element changes from dxdydz to
rather than (x,y,z). The
differential volume element changes from dxdydz to
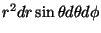 .
.
with
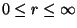 ,
,
 and
and
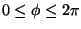 .
.



Next: Differential Equations
Up: Calculus/Integration
Previous: Calculus/Integration
2002-06-14