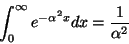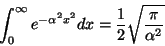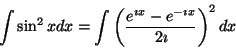Next: Multidimensional Integrals
Up: Math Review
Previous: Calculus/Partial Differentiation
- 1.
- The process of indefinite integration finds a function (F) whose
derivative is a given function (f), call it f(V).
If
then
where C is a constant of integration.
If
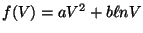 then
then
(since
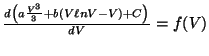 )
where, again, C is a constant of integration (which vanishes upon
differentiation of p(V) to re-obtain f(V).
)
where, again, C is a constant of integration (which vanishes upon
differentiation of p(V) to re-obtain f(V).
- 2.
- The process of definite integration means, given a function f(V) and
two values of V, finding the area under the graph of f(V) between the
aforementioned values of V:
where, of course, the constant of integration cancels.
- 3.
- a special integral is defined:
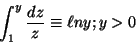
0
\end{displaymath}">
- 4.
- There exist a special set of indefinite and definite integrals which
should be known:
- (a)
-
- (b)
-
- (c)
-
The process of indefinite integration finds a function (F) whose
derivative is a given function (f), call it f(V).
If
then
where C is a constant of integration.
If
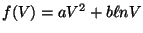 then
then
(since
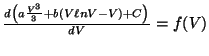 )
where, again, C is a constant of integration (which vanishes upon
differentiation of p(V) to re-obtain f(V).
The process of definite integration means, given a function f(V) and
two values of V, finding the area under the graph of f(V) between the
aforementioned values of V:
)
where, again, C is a constant of integration (which vanishes upon
differentiation of p(V) to re-obtain f(V).
The process of definite integration means, given a function f(V) and
two values of V, finding the area under the graph of f(V) between the
aforementioned values of V:
where, of course, the constant of integration cancels.
a special integral is defined:
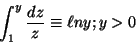
0
\end{displaymath}">
There exist a special set of indefinite and definite integrals which
should be known:
- 1.
-
- 2.
-
- 3.
-



Next: Multidimensional Integrals
Up: Math Review
Previous: Calculus/Partial Differentiation
2002-06-14
![]() then
then
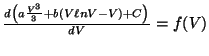 )
where, again, C is a constant of integration (which vanishes upon
differentiation of p(V) to re-obtain f(V).
)
where, again, C is a constant of integration (which vanishes upon
differentiation of p(V) to re-obtain f(V).