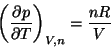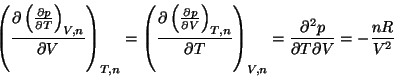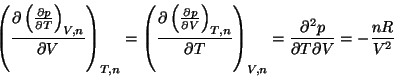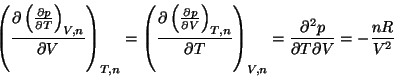Next: Calculus/Integration
Up: Math Review
Previous: DeMoivre's (Euler's) Theorem etc
- 1.
- If f(x,y) is a function of two variables, x and y, then
- (a)
- If
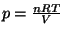 then
then
- (b)
- If
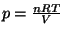 then
then
- (c)
- The double differentiation is order independent, i.e.,
If f(x,y) is a function of two variables, x and y, then
- 1.
- If
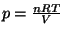 then
then
- 2.
- If
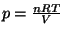 then
then
- 3.
- The double differentiation is order independent, i.e.,
2002-06-14
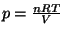 then
then
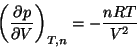
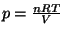 then
then