
where p(a) is the pressure at V=a,
- (a)
- Geometric
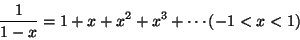
- (b)
- Binomial
There is an error in the following (thanks Mike Daly). It should read 1 + nx + etc..
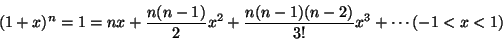
- (c)
- Natural Logarithm (ln)
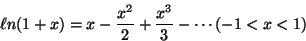
- (d)
- Exponential
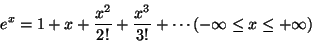
- (e)
- Sin
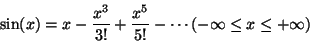
- (f)
- Cos
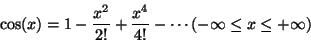

There is an error in the following (thanks Mike Daly). It should read 1 + nx + etc..
