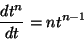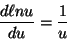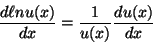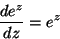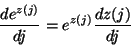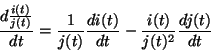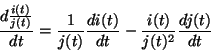Calculus/Differentiation

1.

if p = f(T) then

$$\frac{dp}{dT} = \frac{d f(T)}{dT} = f^\prime (T) = \lim_{h\rightarrow 0} \frac{f(T+h)-f(T)}{h}$$

Thus, if p = T² then

$$\frac{dp}{dT} = \lim_{h\rightarrow 0} \frac{(T+h)^2-T^2}{h} = \frac{T^2 +2hT +h^2-T^2}{h} = \frac{2hT+h^2}{h} \rightarrow 2T$$

From this it follows that

(a)

$$\frac{d t^n}{dt} = nt^{n-1}$$

(b)

$$\frac{d \ell n u}{du} = \frac{1}{u}$$

and

$$\frac{d \ell n u(x)}{dx} = \frac{1}{u(x)}\frac{du(x)}{dx}$$

(c)

$$\frac{d e^z}{dz} = e^z$$

and

$$\frac{d e^{z(j)}}{dj} = e^{z(j)}\frac{dz(j)}{dj}$$

2.

if h(t) and g(t) are functions of t, then

$$\frac{d (h(t)\times g(t))}{dt} = \frac{dh(t)}{dt}g(t) + \frac{dg(t)}{dt}h(t)$$

3.

if i(t) and j(t) are functions of t, then

$$\frac{d \frac{i(t)}{j(t)}}{dt} = \frac{1}{j(t)} \frac{d i(t)}{dt} - \frac{i(t)}{j(t)^2}\frac{dj(t)}{dt}$$

4.

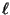if k = $\ell$n(m) and m is a function of of g, i.e., m = m(g), then

$$\frac{dk}{dg} = \frac{d\ell n(m)}{dg} = \frac{d \ell(m)}{dm}\frac{dm(g)}{dg}$$

This is an example of the chain rule.

5.

if y = f(x) has a solution x=g(y) then

$$\frac{dx}{dy} = \frac{1}{\frac{dy}{dx}}$$

6.

$$\frac{ d \sin \alpha}{d \alpha} = \cos \alpha$$

7.

$$\frac{ d \cos \alpha}{d \alpha} = -\sin \alpha$$