Multi Angle Derivations

In a similar vein, from

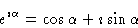$$e^{\imath \alpha} = \cos \alpha + \imath \sin \alpha$$ (1)

and

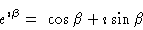$$e^{\imath \beta}= \ \cos \beta + \imath \sin \beta$$ (2)

Multiplication of 1 and 2 yields

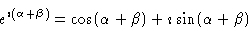$$e^{\imath ( \alpha+\beta )} = \cos (\alpha + \beta) + \imath \sin ( \alpha + \beta )$$ (3)

Multiplication of which also equals

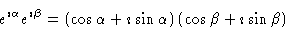$$e^{\imath \alpha} e^{\imath \beta} = \left ( \cos \alpha + ... ...alpha \right ) \left ( \cos \beta + \imath \sin \beta \right )$$ (4)

from which one obtains, equating real and imaginary parts separately, for example,

$$\sin(\alpha+\beta) = \sin \alpha \cos \beta + \sin \beta \cos \alpha$$