


Next: .
Up: Revisiting Woodward Hoffmann Rules
Previous: .
We artificially constrained the geometry to a square, so that
the forming bond would not be canted relative to the emerging bond line
( Had we left the sp2 hybridization of atoms 2 and 3,
the bond angles 1-2-3 and 2-3-4 would be 120o, which would have
forced the p-orbitals on atoms 1 and 4 to approach each other in
canted fashion.
Instead, we force them to 90o so that the forming
bond is 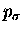 or
or
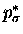 .
This substitutes for the 109.471o expected
if atoms 1 and 4 re-hybridized into sp3.
)
.
The 1-4 Hamiltonian matrix element then is
.
This substitutes for the 109.471o expected
if atoms 1 and 4 re-hybridized into sp3.
)
.
The 1-4 Hamiltonian matrix element then is
Carl David
1999-06-16