


Next: .
Up: Revisiting Woodward Hoffmann Rules
Previous: .
The one-electron Hückel Hamiltonian is
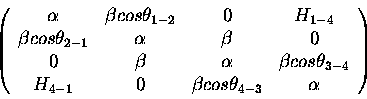 |
(11) |
where, when
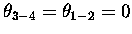 ,
we have maximum overlap.
,
we have maximum overlap.
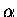 is the standard Hückel <i|H|i> matrix element.
Notice that as
is the standard Hückel <i|H|i> matrix element.
Notice that as
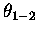 approaches 90o, the
overlap between orbitals on atoms 1 and 4 increases to a maximum,
and the overlap between orbitals on atoms 1 and 2 as well as between 3 and 4
decrease to zero.
Notice further that we need the
approaches 90o, the
overlap between orbitals on atoms 1 and 4 increases to a maximum,
and the overlap between orbitals on atoms 1 and 2 as well as between 3 and 4
decrease to zero.
Notice further that we need the 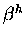 (previously defined) to distinguish between
the nascent
(previously defined) to distinguish between
the nascent 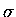 bond forming (1-4) and the destroyed
bond forming (1-4) and the destroyed 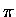 bonds,
(1-2 and 3-4, there is no twist angle for 2-3).
bonds,
(1-2 and 3-4, there is no twist angle for 2-3).
Technically, we can now plot the energy as a function of the reaction coordinate (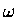 ).
The con- and dis-rotatory aspects are obtained by choosing the previously noted relation between
the relevant angles, i.e.,
).
The con- and dis-rotatory aspects are obtained by choosing the previously noted relation between
the relevant angles, i.e.,
or
Carl David
1999-06-16
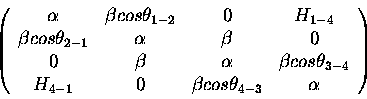
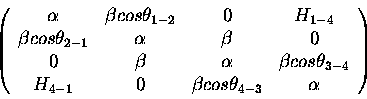
![]() ).
The con- and dis-rotatory aspects are obtained by choosing the previously noted relation between
the relevant angles, i.e.,
).
The con- and dis-rotatory aspects are obtained by choosing the previously noted relation between
the relevant angles, i.e.,