

Next: Form of the Up-Ladder
Up: A Ladder Operator Solution
Previous: Introduction
We start by remembering the trigonometric definition of the sine of the sum
of two angles, i.e.,
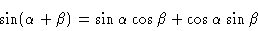 |
(1) |
We seek an operator, M+ which takes a state |n> and ladders it up to
the next state, i.e., |n+1>.
Since the particle in a box problem is already solved, i.e., we know that |n> is
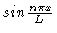 we can employ this knowledge to construct our ladder operators.
Symbolically, we define the up-ladder operator through the statement
we can employ this knowledge to construct our ladder operators.
Symbolically, we define the up-ladder operator through the statement
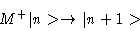
\rightarrow \vert n+1>
\end{displaymath}">
and we will require the inverse (the down-ladder operator), i.e.,
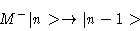
\rightarrow \vert n-1>
\end{displaymath}">
where the down-ladder operator is lowering us from n to n-1 as usual.
One knows that there is a lower bound to the ladder, i.e., that one can not ladder
down from the lowest state (n=1), i.e.,
M-|lowest> = 0
1998-05-13