


Next: Ladder Operator for Angular
Up: Alternative Formulations for Angular Operators
Previous: .
which is, ultimately
![\begin{displaymath}L^2 = -\hbar^2
\left (
\frac{1}{\sin^2\theta}
\left [
\sin \t...
...\theta}
+ \frac{\partial^2}{\partial \phi^2}
\right ]
\right )
\end{displaymath}](img73.gif) |
(32) |
We see that the operator associated with
Legendre's Equation (multiplied by a constant)
has emerged, meaning that Legendre Polynomials
and angular momentum are intimately asssociated together.
2001-12-26
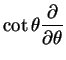
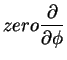
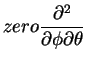
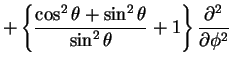
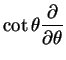
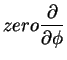
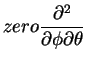
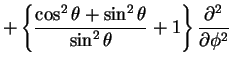
![\begin{displaymath}L^2 = -\hbar^2
\left (
\frac{1}{\sin^2\theta}
\left [
\sin \t...
...\theta}
+ \frac{\partial^2}{\partial \phi^2}
\right ]
\right )
\end{displaymath}](img73.gif)