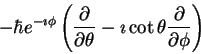
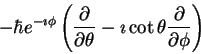
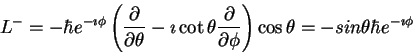
To clinch the example, let's up ladder on
![]() .
For the up laddering we have
.
For the up laddering we have
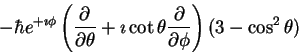 |
(49) |
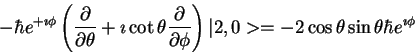 = -2 \cos \theta \sin \theta\hbar e^{\imath \phi}
\end{displaymath}">
= -2 \cos \theta \sin \theta\hbar e^{\imath \phi}
\end{displaymath}"> |
(50) |
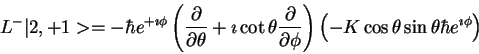 = -\hbar e^{+\imath \phi}
\left (
\frac{\parti...
...left ( -K \cos \theta \sin \theta\hbar e^{\imath \phi}\right )
\end{displaymath}">
= -\hbar e^{+\imath \phi}
\left (
\frac{\parti...
...left ( -K \cos \theta \sin \theta\hbar e^{\imath \phi}\right )
\end{displaymath}">