.

(*restored equation*)

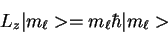
$$L_z \vert m_\ell> = m_\ell \hbar\vert m_\ell>$$ = m_\ell \hbar\vert m_\ell> \end{displaymath}">

then

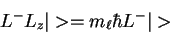
$$L^- L_z \vert> = m_\ell \hbar L^-\vert>$$ = m_\ell \hbar L^-\vert> \end{displaymath}">

or

$$[L_z L^- + \hbar]\vert> = m_\ell \hbar L^-\vert>$$ = m_\ell \hbar L^-\vert> \end{displaymath}">

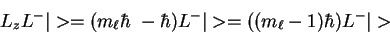
$$L_z L^- \vert> = ( m_\ell \hbar \ - \hbar ) L^-\vert> = ( (m_\ell - 1)\hbar ) L^-\vert>$$ = ( m_\ell \hbar \ - \hbar ) L^-\vert> = ( (m_\ell - 1)\hbar ) L^-\vert> \end{displaymath}">

which means that where ever we were, we are now lower by 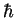$\hbar$.

On the other hand, had we used L⁺ we would have gone to 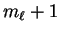$m_\ell+1$, i.e., laddered up. One sees where the name ``ladder operator'' came from.

Next, we need an expression for L⁺L^-, not the commutator. It is:

$$L^+L^- = (L_x+\imath L_y)(L_x - \imath L_y)$$

$$=L_x^2 + L_y^2 + \imath (L_yL_x - L_xL_y)$$

or

$$=L_x^2 + L_y^2 +L_z^2 + \imath (L_yL_x - L_xL_y) - L_z^2$$

or

$$=L_x^2 + L_y^2 +L_z^2 + \imath (-\imath \hbar L_z) - L_K^2$$