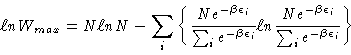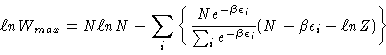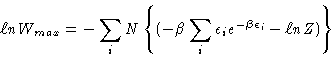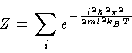

Next: About this document ...
Interpreting the Boltzmann Distribution and the First Law of Thermodynamics
We know that
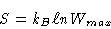 |
(1) |
where
in which the energy level occupation numbers are
those which describe equilibrium, i.e.,
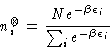 |
(2) |
As usual, using Stirling's approximation, we have
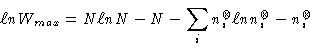 |
(3) |
where we note in passing that
(whether we are in the equilibrium state or not) results in a fortuitous
cancellation.
Substituting the equilibrium populations (Equation 2)
into the occupation numbers of Equation 3
we obtain
which us
which is
where, of course,
so that
where, we know that
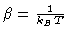 .
.
Therefore, cross multiplying by T we have
or
This fundamental identification of the Helmholtz
Free Energy with the partition function shows that A (and Z)
are functions of temperature and volume.
Now, for a one dimension gas (where L will serve instead of V),
we know that the energy levels are given by the quantum mechanical
formula
Since the energy levels are themselves functions of the volume
(here length, L), it is apparent that when one substitutes
these energy levels into the partition function that one generates
a function of T and L (or V, if you will):
Further, as all elementary treatments show, this partition function leads
to the average thermal energy being E=(1/2)NkBT, where, had we done
the derivation in three dimensions, we would have had (3/2)NkBT.
This, of course, is a triumph of the statistical mechanical theory.
But, from thermodynamics, we had
dE = dq + dw
and from statistical thermodynamics we now have
and we see that there are two ways to change the energy in this
last expression, changing the energy levels themselves, or changing
the occupation numbers.
Thus
The first term corresponds to heat (dq), and the second term corresponds to work (dw).
What a spectacular clarification.
Keeping systems in their individual energy levels but allowing those levels to
shift corresponds to external work of some kind.
Keeping the energy levels fixed and shifting the populations of those energy levels
corresponds to heating (or cooling).
Adiabatic processes correspond to processes in which the populations are maintained
constant.
Heat addition (or subtraction) results in population changes, while work
(either performing it or having it performed on the system) results in changes
in the energy levels themselves.


Next: About this document ...
1998-04-17