Legendre Transformations (III, The Sackur-Tetrode Equation)

When one¹ writes

$$E = \frac{3}{2} N k_BT$$ (1)

for an ideal (monatomic) gas, where k_B is the Boltzmann constant, it certainly looks like the energy is a function of T, the temperature. (N is the number of molecules, and E is the first law thermodynamic energy.)

But we are taught that E=E(S,V), and while it is true (from the Joule expansion argument), that for an ideal gas, E=E(S) alone, i.e., the energy does not depend on the volume, never the less, one wonders how to reconcile these two views, that on the one hand, the energy should be a function of S, and yet it explicitly is written as a function of T in Equation 1. How is one to write

$$dE = TdS - p dV = TdS (for\ an\ ideal\ gas)$$

using Equation 1 above?

Even if one were willing to say that E is a function of T through S, i.e., S= S(T,V) and E=E(S), what are we to do with Equation 1 to construct the Helmholtz free energy (and the Gibbs)?

The Sackur-Tetrode Equation gives us some insight into this problem. Specifically, this equation is

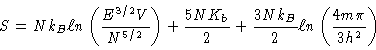$$S = N k_B \ell n \left ( \frac{E^{3/2}V}{N^{5/2}} \right ) + ... ...2} + \frac{3Nk_B}{2}\ell n \left ( \frac{4m\pi}{3h^2} \right )$$ (2)

i.e., S = S(E,V) and assorted atomic constants ². For clarity, we absorb these constants (lump them) so the Sackur-Tetrode Equation becomes

$$S = Nk_B \ell n \left (E^{3/2}V \right ) + \beta$$ (3)

where $\beta$ absorbs Planck's constant, the mass of the atomic constituent of the ideal gas, $\pi$, etc..

We can invert Equation 3 solving for E in terms of S and V, obtaining

$$E = \left ( \frac{e^{(S-\beta)/Nk_B}}{V} \right )^{3/2}$$

which surely reflects the desired dependency on S and V.

This form begs us to take the partial derivative of E with respect to S at constant V, to see what happens. Thus

$$\left ( \frac{\partial E}{\partial S} \right )_V = \frac{2}{3} \frac{E}{Nk_B} \equiv T$$

which recovers $E=\frac{3}{2}Nk_BT$ (Equation 1).

As an aside, we obtain the other partial derivative

$$\left ( \frac{\partial E}{\partial V} \right )_S = - \frac{2}{3} \frac{E}{V} \equiv -p$$

which recovers a well known result for ideal gases.

In the set of variables S, T, p, and V the form of the partial derivatives is simplest if one chooses two of them appropriately, the so called canonical variables.

Choosing E(T,V) is not useful, since the partial of E with T at constant V has no special meaning, i.e., does not lead to another member of the set. Choosing E = E(S,V), on the other hand, leads to something wonderful since the partial of E with respect to S leads to T, a member of the set.

The variable pairs S and T on the one hand, and p and V on the other are known as cannonically conjugate variables ³. Posing thermodynamic equations in properly chosen cannonical pairs (one from each pair) results in equations whose information content is maximum, and whose applicable partial derivatives are themselves cannonically conjugate opposites.

Special thanks to Mark DiCocco, Yale Med, who has been reading, critcally, lots of the stuff on this site, and telling me when I'm wrong.