Legendre Transformations (II, An example)

Consider a system whose energy has the form:

E = 2S² + 4 + V² = E(S,V)

where E is an explicit function of S and V (as required in elementary thermo). At constant V, we have

$$\left ( \frac{\partial E}{\partial S}\right )_V = 4 S = slope$$

 

Figure 1: E(S) is parabolic in S, as is A(T) in T, via the Legendre Transformations

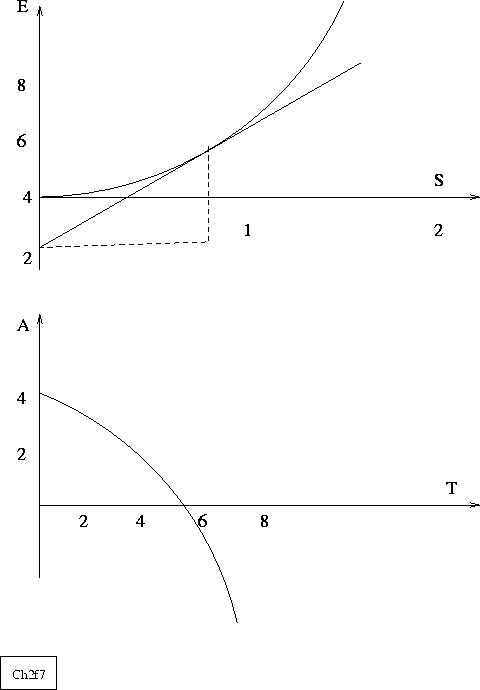We wish to perform a Legendre Transformation on E(S,V) to change the S variable to something else (it's going to be the temperature). We wish

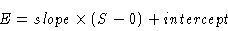$$E = slope \times (S-0) + intercept i$$ (1)

Since the slope is 4S (see above) we have S=slope/4, so that, substituting into equation 1 we have

$$E = slope \times (S-0) + intercept = slope \times \frac{slope}{4}+intercept$$

so that

$$2S^2 + 4 + V^2 = \frac{slope^2}{4}+intercept$$

which is, substituting (slope/4) for S on the left hand side

$$2 \left ( \frac{slope}{4} \right )^2 + 4 + V^2 = \frac{slope^2}{4}+intercept$$

which is an equation for the intercept as a function of the slope (and V, which is being carried along here):

$$intercept = V^2 + 4 - \frac{slope^2}{8}$$

If we call the intercept A, the Helmholtz Free Energy, and the slope we call T, the temperature, then we have

$$A(T,V) = V^2 + 4 - \frac{T^2}{8}$$

which is the desired result. That is, we have started with a function of S and V and ended up with a function of T and V.

Just to prove that we know what we're doing, we will do it again, this time transforming A(T,V) into E(S,V). We start with desiring a representation of A(T,V) of the form:

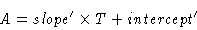$$A = slope ' \times T + intercept '$$ (2)

Then

$$\left ( \frac{\partial A}{\partial T} \right )_V = -2T/8 = slope '$$

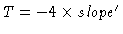i.e., $T = -4\times slope '$. Substituting for T in equation 2

$$A = slope ' \times T + intercept ' = slope ' \times (-4 \times slope ') + intercept '$$

which is, substituting on the l.h.s.

$$V^2 + 4 - \frac{T^2}{8} = slope ' \times (-4 \times slope ' ) + intercept '$$

which is, again substituting for T,

$$V^2 + 4 - \frac{(-4 \times slope ' )^2}{8} = slope ' \times (-4 \times slope ') + intercept '$$

which rearranges to

$$V^2 + 4 + 2 \times slope '^2 = intercept '$$

i.e.

$$V^2 + 4 + 2 \times S^2 = E$$

which is what we started with (sorry about the sentence construction).