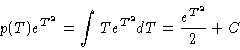

Next: About this document ...
Up: Differential Equations
Previous: First Order, Variable Separable
A differential equation of the form
where g(T) and q(T) are known, i.e., given functions, and
p(T) is the desired solution, a function of T, can be solved
using integration factors.
We note that multiplying by a factor (so far unknown) h(T), one would have
which could be rewritten as
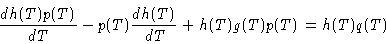 |
(5) |
If the second and third terms could be made to cancel, i.e., if
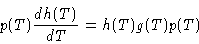 |
(6) |
the resulting differential equation (5) would read
which would be integrable.
But p(T) cancels from both sides of the equation (6)
so, dividing both sides by h(T) and multiplying both sides by dT and integrating one has
Integration of the left hand side gives
that is
which is, acutally, a formula for h(T).
As an example consider the first-order equation
where g(T) = 2T and q(T) = T.
One has
so
so
Cancelling, one has
Finally, solving for p(T) produces
One now uses the initial condition to finish.
Thus p(1) = 3
giving an equation for C.


Next: About this document ...
Up: Differential Equations
Previous: First Order, Variable Separable
1998-05-11