Solutions 1 of the Schrödinger equation yield energy levels. You define the system, which ultimately defines the potential energies and the boundary conditions, and the Schrödinger scheme will generate (usually approximately) the relevant energy levels.
Now, given an aasembly of these systems, how many systems occupy each of these energy levels depends on the temperature and external conditions, and is governed by the Maxwell Boltzmann distribution. A derivation of that distribution without using the Lagrange method of undetermined multipliers is re-presented.
Knowing the Energy Levels of a system, i.e.,
![]() and given a set of occupation numbers for these energy levels,
and given a set of occupation numbers for these energy levels,
![]() ,
where the two subscripts are linked together, i.e.,
the occupation number tells the number in the energy level with the same
value of `i', we seek the maximum in the
,
where the two subscripts are linked together, i.e.,
the occupation number tells the number in the energy level with the same
value of `i', we seek the maximum in the ![]() ,
or the minimum in
the associated Helmholtz free energy, A.
,
or the minimum in
the associated Helmholtz free energy, A.
First and foremost for this simplified derivation, we assume that the energy levels are non-degenerate2.
Next, we know that
From Equation 5 we have
| (6) |
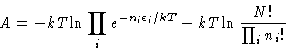 |
(7) |
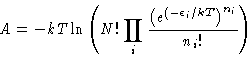
For that state whose occupation numbers minimize A, i.e.
![]() ,
we would have
,
we would have
Choose any two of these `optimally' occupied levels, say 3 and 6, and,
holding all other occupation numbers fixed, raise one and lower the other
by exactly one particle (system).
Then, one would have
Therefore ![]() ,
i.e.,
,
i.e.,
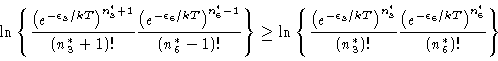 |
(10) |
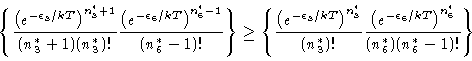 |
(11) |
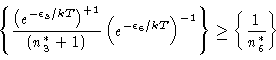 |
(12) |
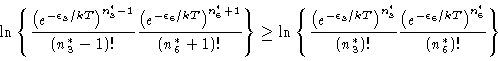 |
(15) |
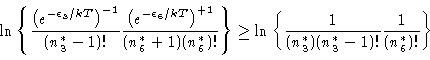 |
(16) |
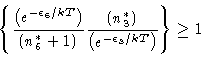 |
(17) |
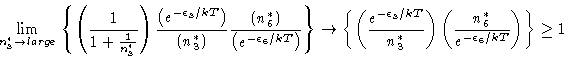 |
(19) |
We have, combining the two (Equations 18 and 20),
This would mean that