.

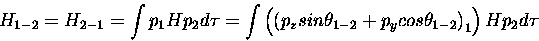$$H_{1-2} = H_{2-1} = \int p_1 H p_2 d\tau= \int \left (\left ... ...a_{1-2} + p_y cos \theta_{1-2} \right )_1 \right ) H p_2 d\tau$$ (4)

which gives

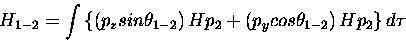$$H_{1-2} = \int \left \{ \left (p_z sin \theta_{1-2} \right )... ... \left ( p_y cos \theta_{1-2} \right ) H p_2 \right \}d \tau$$ (5)

since p₂ is a p_y orbital, which, according to normal usage, is since p₂ is a p_y and ``perpendicular'' (orthogonal) to p_z. 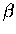$\beta$ is the standard Hückel value assigned for parallel p-orbitals (here p_y).

$$H_{1-2} = \int p_y p_2 cos \theta_{1-2} d\tau= \beta cos \theta_{1-2}$$