

Next: Discussion
Up: A Ladder Operator Solution
Previous: The Commutator of M+ Hop
Then, if
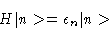
= \epsilon_n\vert n>
\end{displaymath}">
operating from the left with M+ one has
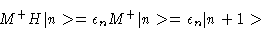
= \epsilon_n M^+\vert n>=\epsilon_n \vert n+1>
\end{displaymath}">
and since
[H,M+] = HM+ - M+H, using Equation 5 one has
![\begin{displaymath}HM^+\vert n>-[H,M^+] \vert n> =\epsilon_n \vert n+1>
\end{displaymath}](img27.gif)
-[H,M^+] \vert n> =\epsilon_n \vert n+1>
\end{displaymath}">
![\begin{displaymath}H\vert n+1>-[H,M^+] \vert n> = \epsilon_n \vert n+1>
\end{displaymath}](img28.gif)
-[H,M^+] \vert n> = \epsilon_n \vert n+1>
\end{displaymath}">
and then, after a tedious amount of algebra, one obtains
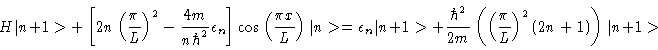
+\left [ 2n
\left ( \frac{\pi}{L}\right )^2
- \f...
... (
\left (\frac{\pi}{L}\right )^2 (2n + 1)
\right )\vert n+1>
\end{displaymath}">
From this we conclude that, if the elements in square brackets cancelled perfectly,
M+|n+1> would be an eigenfunction, i.e.,
if
i.e.,
then
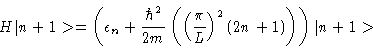
= \left ( \epsilon_n
+ \frac{\hbar^2}{2m} \left ...
... (\frac{\pi}{L}\right )^2 (2n + 1)
\right )\right )\vert n+1>
\end{displaymath}">
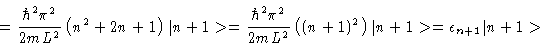
= \epsilon_{n+1} \vert n+1>
\end{displaymath}">
This represents a deluge of results, since we have obtained the redundant
result of the form of the eigenvalue and the form of the next (higher) eigenvalue.
Generally, we have to work a bit harder in ladder operator solutions to quantum mechanical
problems, than we have had to here.
1998-05-13
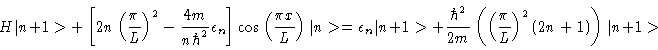 +\left [ 2n
\left ( \frac{\pi}{L}\right )^2
- \f...
... (
\left (\frac{\pi}{L}\right )^2 (2n + 1)
\right )\vert n+1>
\end{displaymath}">
+\left [ 2n
\left ( \frac{\pi}{L}\right )^2
- \f...
... (
\left (\frac{\pi}{L}\right )^2 (2n + 1)
\right )\vert n+1>
\end{displaymath}">
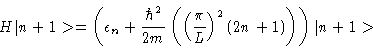 = \left ( \epsilon_n
+ \frac{\hbar^2}{2m} \left ...
... (\frac{\pi}{L}\right )^2 (2n + 1)
\right )\right )\vert n+1>
\end{displaymath}">
= \left ( \epsilon_n
+ \frac{\hbar^2}{2m} \left ...
... (\frac{\pi}{L}\right )^2 (2n + 1)
\right )\right )\vert n+1>
\end{displaymath}">