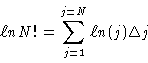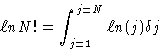

Next: About this document ...
Up: Stirling's Approximation
Previous: Stirling's Approximation
 is the starting point for this derivation, rather than
N factorial (N!) itself.
is the starting point for this derivation, rather than
N factorial (N!) itself.
which can be written as
We now write this backwards:
which covers the same territory.
Figure 1:
The logarithmic factorial sum, shown explicitly.
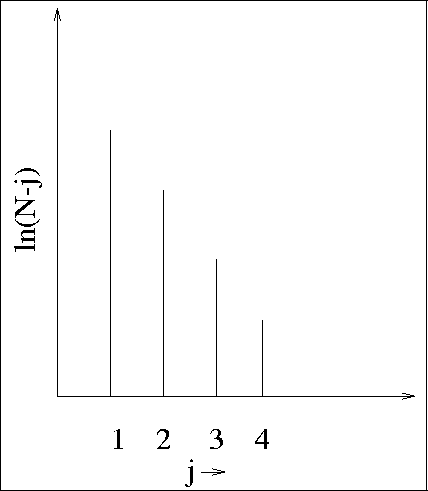 |
Next, we convert this sum to an area by constucting horizontal
bridges (as shown) where the width of each rectangle is going to turn
out to be one (1)!
This means that the height and the area are synonymous!
Figure 2:
The logarithmic factorial sum, reversed.
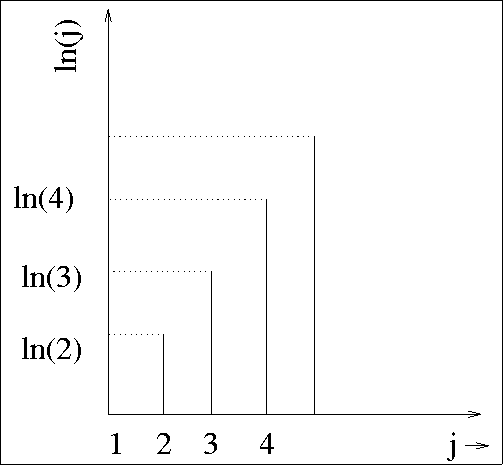 |
We then have
as an area, and we rewrite this as
preparatory to making the histogram to continuous functional area
transformation taught in first year calculus.
Figure 3:
The logarithmic factorial sum, converted to a histogram.
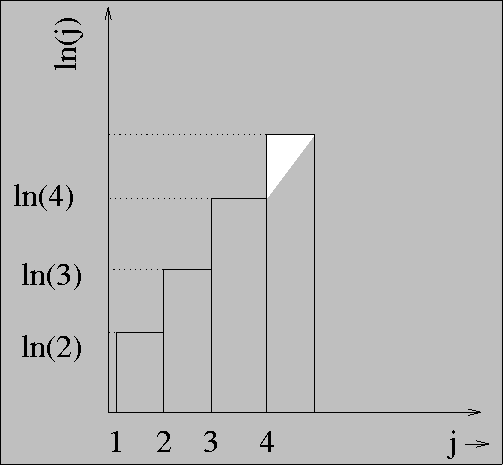 |
We then have
which is trivially integrable to give
which evaluates to
which is, in the limit N much larger than 1


Next: About this document ...
Up: Stirling's Approximation
Previous: Stirling's Approximation
1998-05-22

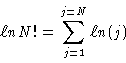
![\begin{displaymath}\ell n N! = \sum_{j=1}^{j=N}\ell n (j) [(j+1)-j]
\end{displaymath}](img8.gif)