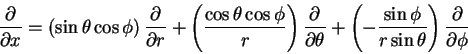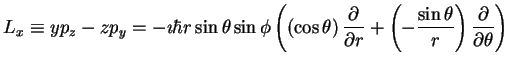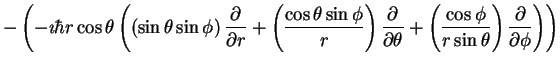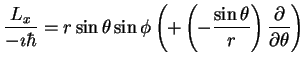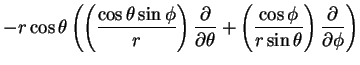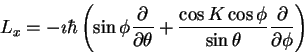.

(restored equation*)

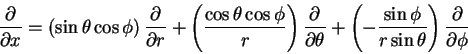$$\frac{\partial}{\partial x} = \left ( \sin \theta \cos \phi\... ...in \phi}{r \sin \theta}\right )\frac{\partial}{\partial \phi}$$ (13)

so,

$$L_x \equiv y p_z - zp_y = -\imath \hbar r \sin \theta \sin \phi \... ...eft (- \frac{\sin \theta} {r} \right )\frac{\partial}{\partial \theta} \right )$$

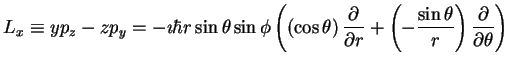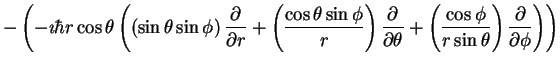$$-\left ( -\imath \hbar r \cos \theta \left ( \left (\sin \theta \... ...os \phi}{r \sin \theta}\right )\frac{\partial}{\partial \phi} \right ) \right )$$ (14)

At constant r, the partial with respect to r looses meaning, and one has

$$\frac{L_x}{-\imath \hbar }= r \sin \theta \sin \phi \left ( + \left (- \frac{\sin \theta} {r} \right )\frac{\partial}{\partial \theta} \right )$$

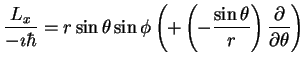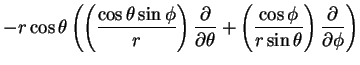$$- r \cos \theta \left ( \left ( \frac{\cos \theta \sin \phi}{r}\r... ... \frac{\cos \phi}{r \sin \theta}\right )\frac{\partial}{\partial \phi} \right )$$ (15)

which leads to (combining the 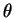$\theta$ partial derivative terms and cancelling the r terms)

$$L_x = -\imath \hbar \left ( \sin \phi \frac{\partial}{\parti... ...\cos \phi}{\sin\theta} \frac{\partial}{\partial \phi} \right )$$