


Next: .
Up: Alternative Formulations for Angular Operators
Previous: .
(*restored equation*)
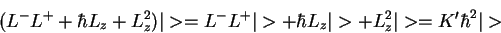
=
L^- L^+\vert> + \hbar L_z\vert> + L_z^2\vert>= K' \hbar^2 \vert>
\end{displaymath}">
If this particular ket is the highest one, |hi>,
so that
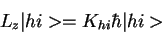
= K_{hi} \hbar\vert hi>
\end{displaymath}">
then laddering up on
it must result in destruction, so we have
if
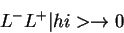
\rightarrow 0
\end{displaymath}">
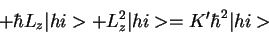
+ L_z^2\vert hi>= K' \hbar^2 \vert hi>
\end{displaymath}">
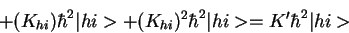
+ (K_{hi})^2 \hbar^2\vert hi>= K' \hbar^2 \vert hi>
\end{displaymath}">
which means that
+ (Khi) + (Khi)2 = K'
while, working down from the low ket (using Equation 44, one has
from
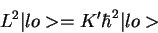
= K' \hbar^2\vert lo>
\end{displaymath}">
by substitution,
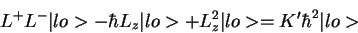
- \hbar L_z\vert lo> + L_z^2\vert lo>= K' \hbar^2 \vert lo>
\end{displaymath}">
which is
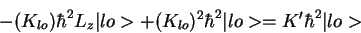
+ (K_{lo})^2 \hbar^2\vert lo>= K' \hbar^2 \vert lo>
\end{displaymath}">
since
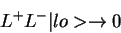
\rightarrow 0
\end{displaymath}">
i.e.,
- (Klo) + (Klo)2 = K'
which means
- (Klo) + (Klo)2 = K' =
+ (Khi) + (Khi)2 = (Klo)((Klo) - 1) = (Khi)((Khi)+1)
which can only be true if (
Klo) = - (Khi).
Say (Klo) = 7, then K' = 7*8 and
-7(-7-1) which is the same!
Note that if (Khi) = 7.1 then (Klo) can not be achieved by
stepping down integral multiples of 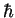 .
Thus if (Khi) were 2.1, then 2.1
.
Thus if (Khi) were 2.1, then 2.1
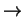 1.1
1.1
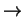 0.1
0.1
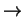 -0.9
-0.9
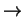 -1.9
-1.9
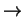 -2.9 which misses -2.1!
-2.9 which misses -2.1!
We conclude from Equation 46 that if (Khi) = 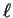 ,
then
,
then



Next: .
Up: Alternative Formulations for Angular Operators
Previous: .
2001-12-26
![]() ,
then
,
then