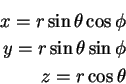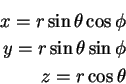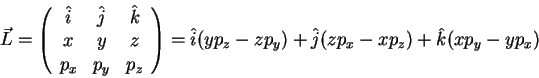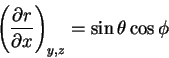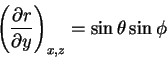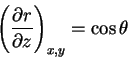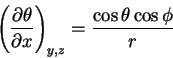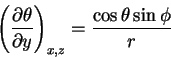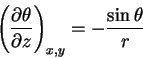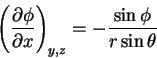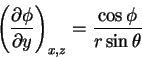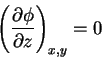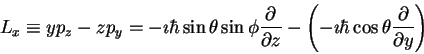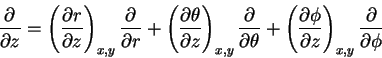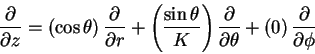Next: .
Up: Alternative Formulations for Angular Operators
Previous: Alternative Formulations for Angular Operators
It is of value to inspect the angular momentum operator
in terms of angles rather than Cartesian coördinates.
Remember that
and
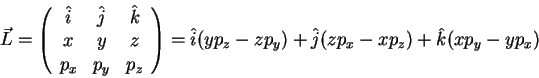 |
(1) |
We start with a feast of partial derivatives:
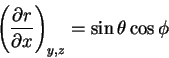 |
(2) |
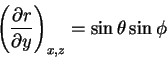 |
(3) |
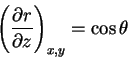 |
(4) |
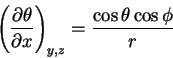 |
(5) |
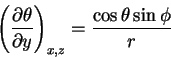 |
(6) |
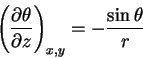 |
(7) |
and finally
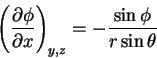 |
(8) |
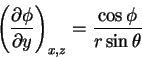 |
(9) |
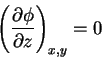 |
(10) |
which we employ on the defined x-component of the angular momentum, thus
where
which is



Next: .
Up: Alternative Formulations for Angular Operators
Previous: Alternative Formulations for Angular Operators
2001-12-26