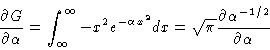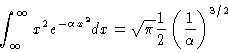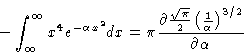

Next: Odd Powers
Up: The Gauss Integral (II)
Previous: The Gauss Integral (II)
The Gauss integral shows up in statistical mechanics, in kinetic theory of
gases, and in elementary statistics, and related integrals are often required.
Define the Gauss integral as
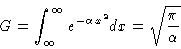 |
(1) |
(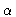 is assumed constant)
and take the dreivative of G with respect to
is assumed constant)
and take the dreivative of G with respect to 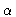 .
We get
.
We get
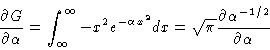 |
(2) |
which means
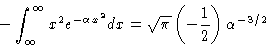 |
(3) |
so
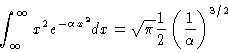 |
(4) |
which is a text-book, table-like result.
We can repeat this again, and obtain
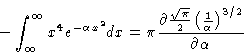 |
(5) |
which would give
and again, and again, so that finally we could see emerging
where n is an integer. This is the form many tables use.


Next: Odd Powers
Up: The Gauss Integral (II)
Previous: The Gauss Integral (II)
1998-06-03