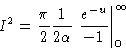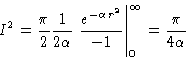

Next: About this document ...
Up: The Gauss Integral
Previous: The Gauss Integral
The Gauss integral shows up in statistical mechanics, in kinetic theory of
gases, and in elementary statistics, and it is worth learning how to do it.
Define the Gauss integral as
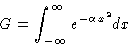 |
(1) |
(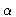 is assumed constant)
and recognize that I (which is G/2) is, by the evenness (is there such a word?)
of the integrand
is assumed constant)
and recognize that I (which is G/2) is, by the evenness (is there such a word?)
of the integrand
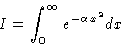 |
(2) |
sufficient, since if we can obtain I, we have G.
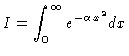 |
|
|
(3) |
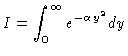 |
|
|
(4) |
so the product of these two is
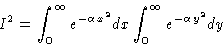 |
(5) |
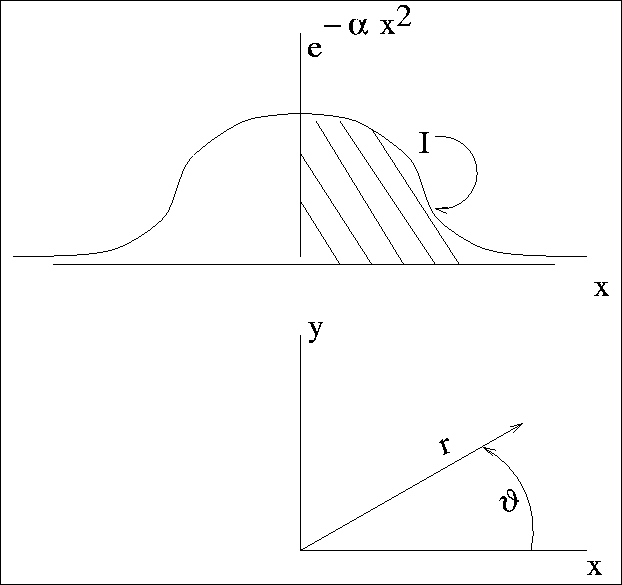
Figure 1:
The Gauss integral.
 |
which we rewrite as
![\begin{displaymath}I^2 = \int_0^\infty dx \left \{ \int_0^\infty
dy \left [ e^{-\alpha x^2} e^{-\alpha y^2} \right ] \right \}
\end{displaymath}](img9.gif) |
(6) |
where we have used many theorems from our freshman calculus days.
Switching to polar coordinates we then have
![\begin{displaymath}I^2 = \int_0^\infty r dr \left \{ \int_0^{\pi/2}
d\theta \left [ e^{-\alpha r^2} \right ] \right \}
\end{displaymath}](img10.gif) |
(7) |
which is
![\begin{displaymath}I^2 = \frac{\pi}{2}\int_0^\infty r dr
\left [ e^{-\alpha r^2} \right ]
\end{displaymath}](img11.gif) |
(8) |
after integration over theta.
This last integral is elementary.
Let
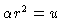 ,
so that
,
so that
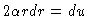 and
and
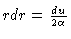 so our remaining integral becomes
so our remaining integral becomes
![\begin{displaymath}I^2 = \frac{\pi}{2} \frac{1}{2 \alpha}\int_0^\infty du
\left [ e^{-u} \right ]
\end{displaymath}](img15.gif) |
(9) |
This means that
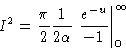 |
(10) |
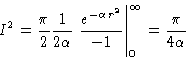 |
(11) |
so, taking the square root, we have
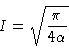 |
(12) |
and since 2I = G, we have
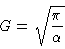 |
(13) |


Next: About this document ...
Up: The Gauss Integral
Previous: The Gauss Integral
1998-05-22
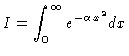
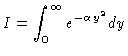
![\begin{displaymath}I^2 = \int_0^\infty r dr \left \{ \int_0^{\pi/2}
d\theta \left [ e^{-\alpha r^2} \right ] \right \}
\end{displaymath}](img10.gif)