y[x] as an example

Consider a function y(x). For the rest of this discussion we will write y[x] rather than y(x) to emphasize the functionality. Anyway, y will be analogous to E, and x will be analogous to V, so that we are doing the constant entropy part of the transformation from dE to dH.

We wish to recast the form y[x] into a new form, $\aleph[y']$, where $\aleph$ is some new function, and y' is $\frac{dy}{dx}$

 

Figure 2: The Legendre Transformation Illustrated

Defining y[x] as a function of x and then forcing a representation of this same function in the form y[x] = m x + b where $m = \frac{dy}{dx} = y'$	If, for example y[x] = ax2 + bx so that $\frac{dy}{dx} = 2a x + b = y'$ then, solving for x in terms of the slope, we obtain $x = \frac{( y'-b)}{2a}$ where, defining $\aleph$ as the intercept, we have:
$y[x] = \frac{dy}{dx} \times x + \aleph$ i.e., $y[x] = y' \times x + \aleph$ where $\aleph$ is the intercept	$y = y' \times x + \aleph$ which is, rearranging: $\aleph[y'] = y[x] - xy'$
$\aleph[y'] \equiv y[x] - xy'$	Substituting $y = ax^2 + bx = slope \times x + intercept$ for x on the left hand side we have: 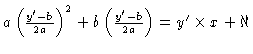$a \left ( \frac{y'-b}{2a}\right )^2 + b \left( \frac{y'-b}{2a} \right ) = y' \times x + \aleph$ and substituting for x on the right hand side we have: 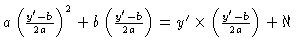$a \left ( \frac{y'-b}{2a}\right )^2 + b \left( \frac{y'-b}{2a} \right ) = y' \times \left ( \frac{y'-b}{2a} \right )+ \aleph$
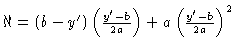
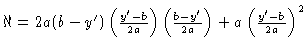
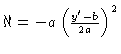
	Solving for $\aleph$ we have $\aleph = (b-y') \left(\frac{y'-b}{2a}\right ) + a \left(\frac{y'-b}{2a}\right )^2$ which is $\aleph = 2a (b-y') \left(\frac{y'-b}{2a}\right ) \left(\frac{b - y'}{2a}\right ) + a \left(\frac{y'-b}{2a}\right )^2$ $\aleph = - a \left(\frac{y'-b}{2a}\right )^2$ where we have expressed $\aleph$ as a function of y'.
$\frac{\partial \aleph}{\partial y'} \equiv \aleph '$	$\frac{\partial \aleph}{\partial y'} -\frac{y'-b}{2a}\equiv \aleph '$ which happens to be -x (see above)
Proof the $\aleph '$ = -x: $\frac{\partial \left (\aleph = y[x] - x\frac{\partial y}{\partial x} \right )}{\partial x}$ and since $\frac{\partial \aleph}{\partial x}= \frac{\partial \aleph}{\partial y'} \frac{\partial y'}{\partial x}$ one has $\aleph' \frac{\partial y'}{\partial x}= y' - y' - x \frac{\partial y'}{\partial x}$ i.e., $\aleph ' = -x$ and therefore $\frac{\partial \aleph}{\partial y'} = \frac{y'-b}{2a} \equiv \aleph ' = -x$ Q.E.D.
Choosing again to write $\aleph$ in an alternate format using a straight line (slope and intercept) we have $\aleph = slope \times y ' + intercept$ which is $\aleph = -x \times y' + intercept$ where the intercept is called "y". Thus, we have $\aleph = -x \times y' + y$ so $y = \aleph + y' \times \aleph '$	$\aleph = \aleph ' \times y ' + intercept$ $\aleph = -x \times y' + intercept$ where the intercept is called "y". Then we have 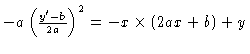$\aleph = -x \times y' + y$ $-a \left ( \frac{y' -b}{2a} \right )^2= -x \times (2ax +b) + y$ $-a x^2 = -x \times (2ax +b) + y$ which is exactly the original defining equation for y[x]!

 

Figure 3: Constructing the Legendre Transformation (II)