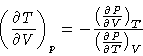

Next: Differential Equations
Up: Functions of 2 or
Previous: Finite Changes in Many
Along a contour of constant p,
when T=f(V) or V=g(T) so that the locus of acceptable
V and T results in p staying constant,
i.e.,
P(T,V) = C,
since p is constant.
Then,
so
after algebraic manipulations and appropriate limit taking.
1998-05-11